UZAYIN ŞEKİLLERİ Asırlık Poincare Savı'nın ispatı için vaadedilmiş olan 1 milyon dolarlık ödülü, belki de Rus ma­tematikçi Grigori Perelman alacak. Matematikçi, ispatı gerçekleştirmekle üç boyutlu uzaylar ka­talogunu da tamamlamış bulunuyor.

raberce bir 4-manifold oluşturur.) Matematikçiler 3-manifoldlar konu­sunda birçok şey biliyorlar; ama en temel bazı soruları yanıtlamak hiç de kolay ol­madı. Manifoldları inceleyen matematik dalı, topoloji. Topologların 3-manifold konusunda sorabilecekleri bazı sorular şunlar: Yapısı en az karmaşık, en basit 3-manifold ne? Aynı ölçüde basit başka bir­çok kuzeni var mı; yoksa tek mi? İlk sorunun yanıtı uzun süredir bilini­yor: 3-küre olarak adlandırılan uzay, en basit kompakt ("tıkız") 3-manifolddur. (Kompakt olmayanlar, sonsuz olan, ya da bir kenarı olan manifoldlar olarak dü­şünülebilir. Burada yalnızca kompakt manifoldları ele alacağız.) Daha sonraki iki soruysa yüz yıl boyunca çözüm bekle­di. Son olarak 2002 yılında Rus matema­tikçi Grigori ("Grisha") Perelman tarafın-

tiğini söyler. Dünya yakınında bu üç sayı enlem, boylam ve yükseklik olabilir. Newton fiziği ve geleneksel kuantum fiziği, her şeyin yer aldığı üç boyutlu uza­yın sabit ve değişmez olduğunu kabul eder. Buna karşın, Einstein'ın genel gö­relilik kuramına göre uzay aktif bir oyun­cudur: bir noktadan bir başkasına olan uzaklık, yörede varolan madde ve enerji miktarıyla ve geçmekte olan herhangi bir kütleçekim dalgası olup olmamasıyla da bağlantılıdır. Ne var ki, sözkonusu olan ister Newton İster Einstein fiziği olsun, uzay, sonlu ya da sonsuzluğundan ba­ğımsız olarak, bir 3-manifold ile temsil edilir. Bu nedenle, 3-manifoldların Özel­liklerini anlamak, tüm fiziğin (ve tüm di­ğer bilimlerin) temelini tam olarak anla­mak bakımından zorunludur. (4-mani-foldlar da önemlidir: uzay ve zaman be-

yağa kalkın ve çevrenize ba­kın. Sıçrayın, ileri-geri yürü­

yün. Kollarınızı sallayın. Siz, her- doğrultuda milyar-

larca ışık-yılına uzanan bir 3-manifoldun (üç boyutlu uzayın) ufak bir bölgesinde hareket eden bir parçacık­lar topluluğusunuz. Manifoldlar (ya da çok katlılar, çok boyutlular) matematiksel yapılardır. Gali­leo ve Kepler'den bu yana fiziğin en bü­yük başarısı, gerçekliği şu ya da bu tür matematikle (örneğin manifoldların ma-tematiğiyle) açıklamasıdır. Fizik, bütün olguların üç boyutlu uzay arka zeminin­de yer aldığını kabul eder (sicim kuram­cılarının bu üç boyut dışında çok küçük boyutların varolduğu savlarını dikkate almazsak). Üç boyut, bir parçacığın ko­numunu saptamak için üç sayının gerek- BİLİM veTEKNİK 66 Aralık 2004

Üniversitesi'nde bu çalışma konusunda bir dizi seminer vermek için Amerika'ya gitti. Bir düzineye yakın kuruluşun önde gelen matematikçilerinden oluşan ekip­ler, makaleleri incelemeye başladılar. Her ayrıntının doğruluğunu inceliyor ve olası hataları arıyorlardı. Perelman, Stony Brook'da iki hafta boyunca günde üç İla altı saat ders verdi, konuşmalar yaptı. Stony Brook matema­tikçisi Michael Anderson'un izlenimleri şöyle: "Her soruyu kesin ve açık biçimde yanıtladı. Ve şimdiye kadar ciddi kuşku­lar öne sürülmüş değil. İspatın tamam­lanması için gereken tek şey, görece kü­çük bir ispat. Ama sonuçtan kimsenin pek kuşkusu yok." İlk makale temel fikir­leri İçeriyor; doğruluğu da kabul edilmiş durumda. İkinci makalenin içeriğiyse uy­gulamalar ve daha teknik görüşler içeri­yor; doğrulanmışlık düzeyi, birincinin ulaştığı düzeye henüz varabilmiş değil. Poincare savının ispatı için 1 milyon dolar ödül konmuş durumda. Bu, Cam­bridge, Massachusetts'teki Clay Matema­tik Enstitüsü'nün 2000 yılında belirledi­ği yedi "Milenyum Problemi'nden biri. Perelman'ın ödülü alabilmesi için ispatın yayınlanması ve iki yıllık bir inceleme sü­resini başarıyla geçmesi gerekiyor. (Ens­titü, çalışmanın web sitesinde yayınlan­masından sonra, sonucun başka herhan­gi bir makale kadar ciddi ve dikkatlice İn­celenmiş olduğuna da karar verebilir.) Perelman, yaptığı çalışmayla, 1990'larda Columbia Üniversitesi'nden Richard S. Hamilton'un yönettiği bir araştırma programını genişleterek ta­mamlamış oluyor. 2003 sonlarında Clay Enstitüsü Hamilton'un çalışmasını bir araştırma ödülüyle onayladı. Perel­man'ın hesapları ve analizleri, Hamil­ton'un karşılaştığı ve üstesinden geleme­diği birkaç engeli ortadan kaldırıyor. Eğer ispatı herkesin de beklediği gibi doğruysa, Perelman gerçekte Poincare savından çok daha geniş bir çalışmayı gerçekleştirmiş olacak. Şimdi Cornell Üniversitesi'nde olan William P. Thurs-ton'un İleri sürmüş olduğu Thurston geometrikleştirme savı, olanaklı bütün 3-manifoldlar için tam bir sınıflandırma. Tekniği ve basitliğiyle inanılmaz 'güzel­likteki' 3-küre, bu harikulade sınıflandır­manın dayanak noktası. Poincare savı yanlış olsaydı -yani küre kadar "basit" başka uzaylar da varolsaydı- 3-manifold-ların sınıflandırılması Thurston'un öner­diğinden sonsuz kat daha karmaşık olur-

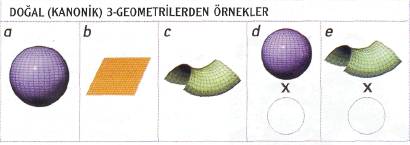
dan sunulan çözümse, Poincare savı ola­rak bilinen kuramı büyük olasılıkla İspat­lamış bulunuyor. Bundan tam 100 yıl önce, Fransız ma­tematikçi Henri Poincare'nin ileri sürdü­ğü sav şu: 3-manifoldlar arasında yer alan 3-küre, benzersizdir; başka hiçbir 3-manifoldun bu denli 'basit' özellikleri yoktur. Daha karmaşık olan 3-manifold­lar, tuğladan bir duvar gibi yukarıya yük­selen sınırlara, ya da bir ormanda önce ayrılıp sonra birleşen patikalar gibi, bir bölgeden diğerine uzanan birden fazla bağlantıya sahiptir. Poincare savı, bu tür­den bir karmaşıklığı olmayan yegane 3-manîfoldun 3-küre olduğunu İleri sürer. Küreyle bu nitelikleri paylaşan herhangi bir üç boyutlu nesne, 3-küreyle aynı biçi­me sokulabilir; topologlar için bu nesne 3-kürenin yalnızca bir başka kopyasıdır. Perelman'ın ispatı, aynı zamanda üçün­cü soruyu da yanıtlayarak varolan bütün 3-manifold tiplerinin sınıflandırılmasını tamamlıyor. 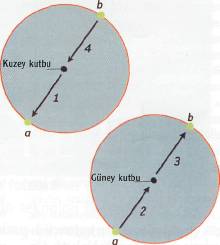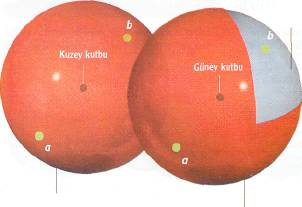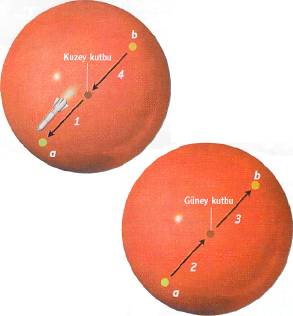Bir 3-kürenin neye benzediğini tasar­lamak biraz beyin jimnastiği gerektiriyor. (Bu, sözcük anlamıyla bir küre değil.) 3-küre, hepimizin bildiği 2-kürenin birçok özelliklerini taşır: küre şeklinde bir lastik balonun lastiği, bir 2-küre oluşturur. 2-küre iki boyutludur; çünkü üzerindeki bir noktanın konumunu belirlemek için iki koordinat (enlem ve boylam) yeterli­dir. Ayrıca, eğer balonun yüzeyinden çok küçük bir disk alıp onu bir büyüteçle İn­celerseniz düz, İki boyutlu bir lastik düz­lemden kesilmiş gibi görünür. Yalnızca çok az bir eğriliğe sahiptir; balon, üstün­de yürüyen ufak bir böcek için bir düz­lem gibi algılanır. Ancak böcek, bir doğ­ru gibi algıladığı bir çizgi üstünde yete­rince yürürse, sonunda başladığı nokta­ya gelir.

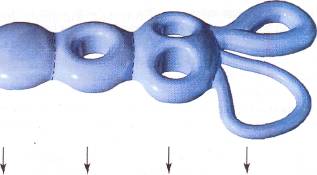
Benzer şekilde, 3-kürede bir sinek, (ya da evrenimiz kadar büyük bir 3-küre­de, bir insan!) kendisini, ''bildiğimiz" üç boyutlu uzaydaymış gibi algılar. Ancak herhangi bir doğrultuda bir doğru üze­rinde uzaya uçtuğunda, sonunda 3-küre-yi çepeçevre dolaşarak kendisini başladı­ğı noktada bulur; tıpkı balon üstündeki sinek, ya da dünya turuna çıkan biri gibi. Üçten farklı boyutlarda küreler de var. 1-küreyi biliyoruz: yalnızca bir çem­ber (yuvarlağın kendisi değil, kenarı), n-boyutlu küreye de n-küre deniyor.

Savların İspatı

Poincare 3-küre savını önerdikten sonra, ispatı konusunda hiçbir ilerleme kaydedilmeksizin yarım yüzyıl geçti. 1960'larda matematikçiler savın beş ya da daha fazla boyutlu küreler için ben­zerlerini ispatladılar. Bu boyutların her biri için, n-küre yegane ve en basit mani-folddur. İspatın, üç ve dörtten büyük bo­yutlar için daha kolay olması, çelişki gibi görünüyordu. Özellikle zor olan dört bo­yut için ispat, 1982'de geldi. Geriye yal­nızca Poincare'nin ilk savı olan 3-küre kalmıştı. Üç boyut probleminin çözümündeki ilk büyük aşama, 2002 Kasımında St. Pe-tersburg'daki Steklov Matematik Ensti-tüsü'nden geldi. Matematikçi Perelman, fizikçi ve matematikçilerin yeni araştır­malarını gönderdikleri www.arxiv.org. web sunucusuna bir makale göndermişti. Çalışma Poincare savından söz etmese de, makaleyi gören topoloji uzmanları onun savla ilgili olduğunu hemen anladı­lar. Bunu 2003 Martındaki ikinci bir ma­kale izledi. O yılın Nisan ve Mayıs ayla-rında Perelman Amerika'daki Massachu­setts Teknoloji Enstitüsü ve Stony Brook

Aralık 2004 67 BİLİM ve TEKNİK

Kürelerin Çok Boyutlu Müziği

Perelman savının kalbinde yatan 3-küreyi göz önüne getirmek için biraz çaba gerekiyor. Büyük boyutlu uzaylar konusunda teorem­ler ispatlayan matematikçiler, buna gerek duymaz. Onlar soyut özel­likler ve daha düşük boyutlarla benzetmelere ve sezgiye dayalı kav-

ramlarla yetinirler (ama tabii benzetmelerin gerçek olmadığını unut­mazlar). Ancak başkaları da, bilinen daha küçük boyutlu örnekler­den yola çıkarak daha yüksek boyutlu nesnelerin neye benzedikleri hakkında fikir sahibi olabilir. 3-küre bu tür bir nesnedir.

1 Bir çemberle çevrelenmiş bir disk düşünelim. Matematikçi için disk "iki bo­yutlu bir top"tur; çember de "bir boyutlu bir küre". Ayrıca, bir "top", bo­yutu ne olursa olsun, beyzbol topu gibi içi dolu bir nesnedir. "Küre" topun yüzeyidir (balon gibi). Çember bir boyutludur; çünkü üstündeki bir konumu belirlemek için tek bir sayı yeterlidir.

.iki boyutlu top

Bir boyutlu küre

2-boyutlu küreyi, diskin İki kopyasından elde edebiliriz. Disklerden birini kuzey yarımküreye benzer bir yarımküreye dö­nüştürün; öteki diski de güney yarımküreye. Sonra da bu iki ya­rımküreyi kenar çizgilerinden yapıştırın. İşte size 2-küre.

2-küre

3 Bir karıncanın kuzey kutbundan yola çıkarak, uluslara­rası gün değişim çizgisiyle İngiltere'deki Green-wich'den geçen boylamın oluşturduğu büyük çember (solda) boyunca yürüdüğünü düşünün. Eğer bu izleği iki disk üzerine (sağda) işaret edersek karıncanın bir doğru boyunca (1) kuzey diskinin kenarına (a) yürüdü­ğünü görürüz. Sonra güney diskinde a'ya karşılık ge­len noktaya geçer ve bu disk üzerinde bir doğru bo­yunca (2 ve 3) yürür. Tekrar kenara geldiğinde (b), kuzey diskine girer ve yürümeye devam ederek başlan­gıç noktası olan kuzey kutbuna (4) doğru yol alır. Ka­rınca 2-küre çevresinde yürürken, İzlediği yolu diskler üzerinde işaretledik. Burada, açıklanması gereken nok­ta, bir diskten ötekine geçtiğinde hareket yönünün ters dönmüş gibi görünmesi.

Ekvator

Güney kutbu

du. Perelman ve Thurston'un sonuçlarıy­la üç boyutlu uzayın alabileceği olanaklı bütün şekillerin; yani evrenimizin (zama­nı değil, yalnızca uzayı ele alarak), mate­matiğin almasına izin verdiği bütün şekil­lerin eksiksiz bir kataloguna sahibiz. Lastik Simitler Poincare savını ve Perelman'ın İspatı­nı daha derinden anlamak İçin topoloji konusunda bazı şeyler bilmek gerekir.

Matematiğin bu dalında nesnenin tam şeklinin önemi yoktur; sanki oyun hamu­rundan yapılmış gibi onu İstediğiniz öl­çüde ezer, gerer, bükersiniz. Sanal oyun hamurundan yapılmış nesnelerle ya da uzaylarla neden ilgileniyoruz? Nedeni, bir nesnenin tam şeklinin -üzerindeki herhangi iki nokta arasındaki uzaklığın-nesnenin "geometrisi'' denen yapısıyla il­gili olması. Topologlar, oyun hamurun­dan yapılmış bir nesneyle, onun geomet­rik yapısından bağımsız olan temel özel-

liklerini keşfederler. Topolojiyle çalış­mak, İnsanların ortak özelliklerini bul­maya benzer; belirli herhangi bir insanın şekline girebilen bir 'oyun hamuru insa-nı'nı ele almak gibi. Topolojinin herhan­gi bir popüler anlatımını okuyanlar, bir topolog için bir fincanla bir simit arasın­da bîr fark olmadığı yolundaki açıklama­yı bilirler. Bununla anlatılmak istenen, oyun hamurundan yapılmış bir fincana, kesmeden, delik açmadan, ya da parçala­rı yapıştırmadan, hamuru bastırıp yuvar­layarak simit şekli verebiliyor olmanız. Öte yandan, bir topu simite dönüştür­mek için ya ortasından delik açmak, ya da onu bir silindir biçiminde uzatıp İki ucu yapıştırmanız gerekir. Bu türden bir kesme ya da yapıştırma gerektirecek olan bu işlemden dolayı, top, topologlara göre bir simitle aynı şey değildir. Topologları en çok ilgilendiren şey,

•Poincare savının ispatı, sonunda genç Rus matematikçisi Grigori Perelman'dan geldi. Pe­relman, çalışmalarıyla, olanaklı bütün 3 boyutlu manifoldları sınıflandıran büyük bir araştırma programını da tamamlamış oluyor. •  Evrenimizin şekli 3-küre olabilir. Bununla ilgili matematiğin, parçacık fiziği ve Einstein'ın görelilik kuramıyla da ilginç bağlantıları var.

Kuşbakışı

• Matematikçiler 100 yıl boyunca, Henri Poincare'nin önerdiği, üç boyutlu küre veya 3-küre olarak bilinen bir nesneyle ilgili savı ispat­lamaya çalıştılar. Sav, 3-kürenin, bütün üç bo­yutlu nesneler, ya da manifoldlar arasında tek olduğunu ileri sürüyor.

BİLİM ve TEKNİK 68 Aralık 2004

Üç boyutlu top

4 Şimdi 2-küreyi ve içerdiği üç boyutlu hacmi ("üç boyutlu bir top") ele alarak çember ve disk ile yaptıklarımızı top ve küreyle de yapalım: Bunların iki kopyasını alıp kenarları birbirine yapış­tıralım. Topları dört boyutta, yarımküre benzeri bir şeye nasıl çarpıtabileceğimizi hayal edemeyiz; ama bu gerekmez de. Yü­zeylerde (2-kürelerde) birbirine karşılık gelen noktaların, tıpkı çemberlerdeki noktalar gibi, birleştirildiğini bilmek yeterli. İki topu birleştirmenin sonucu 3-kuredir; bu küre de dört boyutlu topun "yüzeyi"dir (3-küre ve 4-topun varolduğu dört boyutta, bir nesnenin "yüzeyi" üç boyutludur). Toplardan birine kuzey yarımküre, ötekine de güney yarımküre diyebiliriz. Kuzey kut­bu, kuzeydeki topun merkezindedir (tıpkı kuzey kutbunun, ku­zey diskinin merkezinde olduğu gibi).

Ekvator

5 Şimdi de bu topların, uzayın büyük boş bölgeleri olduğunu ve bir insanın da kuzey kutbundan uzay gemisiyle yola çıktığını dü­şünelim. Sonunda kuzey topunu çevreleyen kürenin tümü olan "ekvatora" (1) ulaşır. Ekvatorda güney yarımküreye geçer ve doğru boyunca giderek onun merkezinden (güney kutbu) yol alarak kendini ekvatorun karşı tarafında (2, 3) bulur. Orada tekrar kuzey yarımküreye geçer ve çıkış noktası olan kuzey kut­buna (4) gelir. Böylece hayalimizde dört boyutlu topun yüzeyin­de hareket ederek onu çepçevre dolaşan bir kişiyi izlemiş ol­duk! İki topun küresel yüzeylerinin birleştirilmesinden oluşan 3-küre Poincare savının geçerli olduğu uzaydır. Evrenimizin şekli de 3-küre olabilir. Bu surece devam ederek beş boyuta (4-küre yapmak için) geçe­biliriz; ancak ne olup bittiğini anlamak daha da zorlaşır. Benzer şekilde iki n-topun kenar noktalarını yapıştırarak belli herhangi bîr n-küreyi oluşturabiliriz. Kenarlar, ya da sınırlar (n-1)-küreler-dir; tıpkı diskin (2-top) kenarlarının bir çember (1-küre) olduğu gibi. Sonuçta (n+l)-topu çevreleyen bir n-küre elde edilir.

20. yüzyıla girildiğinde, en etkin çalış­maları yapan iki matematikçiden biri olan Henri Poincare (diğeri David Hil­bert) bu soruya doğrudan yaklaşmıştı. Poincare'nin, temel ya da uygulamalı ma­tematiğin bütün alanlarına hakim olanla­rın sonuncusu olduğu söylenir. Matema­tiğin bazı alanlarını geliştirmenin yanın­da, gök mekaniği, elektromanyetizma kuramları ve bilim felsefesi konularına (bu konuda çok okunan birkaç kitap da yazmıştı) da katkıda bulunmuştu. Poincare, cebirsel topoloji denen ma­tematik dalının başlıca yaratıcısıdır. 1900 yılı civarında bu yeni alandaki teknikleri kullanarak, bir nesnenin topolojisinin öl­çütü olan ve "homotopi" adı verilen kav­ramı tanımladı ve geliştirdi. Bir manifol-dun homotopisini saptamak İçin bu ma-nifolda kapalı bir ilmek gömdüğünüzü düşünün. İlmek, manifold çevresinde ola-

top ile simitin yüzeyleri; bu nedenle her iki nesnenin içini boşaltarak birer balon olduklarını düşüneceğiz. Bu durumda da topolojileri farklıdır; küresel bir balon, "tor" denen halka şeklinde bir balona dö-nüşemez. Öyleyse tor ve küre, topolojik bakımdan farklı şeylerdir. Başlangıçta to-pologlar, topolojik bakımdan farklı kaç varlık bulunduğunu ve bunları ayırt eden nitelikleri aramaya giriştiler. "Yü­zey" adı da verilen İki boyutlu nesnelerin nitelikleri, açık ve kesin biçimde, yüzeyin "kulp" sayısıyla belirlenir. 19. yüzyıl sonunda matematikçiler yü­zeyleri nasıl sınıflandıracaklarını bulmuş­lardı. Bütün yüzeyler içinde yalnızca kü­renin basit olduğunu biliyorlardı. 3-küre de, 2-küre gibi basitlik bakımından tek miydi? Bu basit sorunun ardından gelen yüz yıllık dönem, yanlış girişimler ve yan­lış ispatlarla dolu.

naklı herhangi bir biçimde sarılabilir. Pe­ki, bu İlmek, hiçbir bölümünü manifold-dan kaldırmadan, yalnızca yer değiştire­rek, bir noktaya sıkıştınlabilir mi? Bir si­mit yüzeyi için, yanıt "hayır"dır. İlmek, si­mitin çevresinde dolanıyorsa bir noktaya sıkıştırılamaz; simitin iç çemberinde en-gelle karşılaşır. Homotopi bir ilmeğin en­gellenebileceği farklı bütün yolların bir ölçümüdür. Bir n-küre üstünde, ilmek ne denli eğilip bükülmüş olsa da, her zaman açı­larak bir noktaya sıkıştırılabilir (bu işlem­ler sırasında ilmeğin kendi içinden geç­mesine de izin veriliyor). Poincare, ola­naklı her ilmeğin bir noktaya büzüşebile­ceği yegane 3-manifoldun, 3-kürenin ken­disi olduğunu ileri sürdü; ama bunu is-patlayamadı. Bu önerme, zamanla "Poin­care savı" olarak ünlendi. On-yıllar bo­yunca birçok kişi savı kanıtladığını bildir-

Aralık 2004 69 BİLİM ve TEKNİK

Yüzeylerin Topolojisi

Topolojide bir nesnenin tıpatıp şekli veya geometrisi önemli değildir. Sanki               tırma yoluyla şekillendirilebilir. Ancak, kesme ve yapıştırma yasaktır. Bu du- her şey oyun hamurundan, ya da lastikten yapılmıştır ve germe, bükme, sıkış-           rumda topolojide, tek deliği olan en soldaki fincan, en sağdaki simite denktir.

Olanaklı bütün 2-boyutlu manifoldlar ya da yüzeyler (kompakt ve yönlendirile­bilir olmak koşuluyla), bir küre alıp (a balonu gibi) ona kulplar ekleyerek ya-

pılabilirler. Bir kulpun ilavesiyle "tür-1 yüzeyi", ya da tor oluşur. Bu, sağ üst­teki simitin yüzeyidir. İki kulp İlavesiyle "tü'r-2 yüzeyi" (b) elde edilir.

foldlar arasında 3-kürenin tek olduğunu söyler: Üstündeki herhangi bir İl­mek, bir nokta oluncaya kadar küçültülebilir; ama başka herhangi bir 3-ma-nifoldda ilmek yakalanabilir; yani bir noktaya büzüşmesi olanaksızdır.

2-küre, yüzeyler arasında benzersizdir; üzerine gömülen kapalı bir ilmek, bir nokta (a) oluncaya kadar küçültülebilir. Buna karşın tor üstündeki bir ilmek, ortadaki delik çevresinde "yakalanabilir" (b). 2-küre dışındaki her yüzeyde il­meğin yakalanabileceği kulplar vardır. Poincare savı, bütün üç boyutlu mani-

a

di; ama yanıldıkları ortaya çıktı. (Burada ve daha sonraki bölümlerde açıklamayı daha anlaşılır kılmak için, karmaşık iki durumu dikkate almıyoruz: yönlendiril©-meyen manifoldlar ve kenarları olan ma­nifoldlar. Örneğin, büküldükten sonra uçları birleştirilmiş bir şerit olan Mobius şeridi yönlendirilemez. Kendisinden bir disk kesilip çıkarılmış olan bir kürenin kenarı vardır. Mobius şeridinin de kena­rı vardır.) Geometrikleştirme Çok dikkatli incelemelere göğüs gere-bilen ilk ispat Perelman'a ait olanı. 3-bo-yutlu manifoldları çözümleme yaklaşımı, geometrikleştirme denen bir süreçle bağ­lantılıdır. Geometri bir nesnenin ya da

manifoldun gerçek biçimiyle ilgilidir: geometri açısından nesne, oyun hamu­rundan değil, seramikten yapılmıştır. Ör­neğin, bir fincanın geometrisi simitinkin-den farklıdır; yüzeyi farklı biçimlerde eğ-rileşir. Simit ve fincan (tek kulplu) topo­lojik bir tor'un, geometrileri farklı iki ör­neğidir. Geometrikleştirmenin Perelman'a ne anlamda yardımcı olduğunu anlamak için, geometrinin 2-manifold ya da yüzey­leri sınıflandırmada nasıl kullanılabilece­ğini ele alalım. Her topolojik yüzeye, eğ­riliğin tümüyle düzgün biçimde yayıldığı özel ve tek olan bir geometri karşılık ge­lir. Küre için, bu yegane geometri, kusur­suzca küresel olan küredir. Topolojik kü­re İçin bir başka örnek de yumurta kabu­ğunun biçimi; ama kabuğun eğriliği her

yerde aynı değil. Yumurtanın sivri ucu, diğer uca göre daha büyük bir eğriliğe sahip. 2-manifoldlar üç geometrik tip oluştu­rur. Küre, "pozitif eğriliğe" sahiptir, bir tümseğin tepesi gibi. Geometrikleştirilmiş simit düzdür; eğriliği düzleminki gibi sı­fırdır. İki ya da daha çok kulpu olan bü­tün diğer manifoldların eğriliği negatiftir. Negatif eğrilik, bir dağ geçidi ya da bir eyerin eğriliğine benzer: Eyer Ön-arka doğrultusunda yukarı doğru, sağ-sol doğ­rultusunda aşağıya doğru kıvrılır. Poin­care, Klein şişesine adını veren Felix Kle­in ve Paul Koebe ile 2-manifoldların bu geometrik sınıflandırılmasına, ya da geo-metrikleştirilmesine katkıda bulunmuştu. Benzer yöntemleri 3-manifoldlara uy­gulamaya çalışmak çok doğal. Her topo-

BİLİM veTEKNİK 70 Aralık 2004

nik") geometriye sahip parçalara ayrılma­sı gerekir. Dahası, 2-manifoldlarda olduğu gibi üç temel geometri yerine, manifold parçalarının her bîri, belirlenmiş 8 doğal geometriden herhangi birinin biçimini ala­bilir. Bir 3-manifoldu parçalara ayırmak, bir bakıma, bir sayının tek bir şekilde asal çarpanlara ayrılmasına benzer. Sınıflandırma yöntemi önce 1970'le-rin sonlarında Thurston tarafından öne­rilmişti. Meslektaşlarıyla birlikte bu savın bazı önemli bölümlerini de ispatladılar. Ne var ki, tüm sistemin dayandığı canalı-cı noktalar, Poincare savı da dahil, erim­leri dışında kaldı. 3-küre tek miydi? Bu sorunun yanıtlanması ve Thurston prog­ramının tamamlanması, ancak Perel­man'ın makaleleriyle mümkün oldu. Bir manifoldu geometrikleştirmek -ya­ni, ona her yerde tek-biçim (uniform) eğ­rilik vermek- için ne yapabiliriz? Bir yön­tem, rasgele bir geometriyle, belki de çe­şitli girinti çıkıntıları olan yumurta kabu­ğu biçimiyle başlamak ve sonra bütün dü­zensizlikleri gidermek olabilir. 1990'ların başında Hamilton, manifoldlar için böyle bir analiz programı başlattı. Matematikçi Gregorio Ricci-Curbastro'nun adıyla anı­lan ve sıcaklık akışını düzenleyen denk­lemle benzerlikleri olan Ricci akışı denk­lemini kullandı. Sıcak ve soğuk noktalan olan bir nesnede doğal olarak sıcaklık her yerde aynı oluncaya kadar, ısı, daha sıcak bölgelerden daha serin bölgelere akar. Ricci akış denklemi, eğrilik üzerin­de benzer etki yaparak bir manifolddaki girinti çıkıntıları eşitler. Bir yumurtayla başlarsanız, yumurta yavaş yavaş kusur­suz küresel biçime dönüşür. Hamilton'un analizi bir engele takıldı: Bazı durumlarda Ricci akışı manifoldun bir bölgesinde, çimdiklenmiş gibi bir nok­taya sıkışıyordu. (Bu, Ricci akışının ısı akışından farklı olduğu durumlardan biri. 'Çimdiklenen' bölgeler sonsuz sıcaklığa yükselmeyi başarabilen noktalara benzi­yordu. Bunun bir örneği, halter biçimin­de, yani ince bir boyunla birleşmiş iki kü­reye benzer bir manifolddu. Küreler bo­yun bölümünü çekerek büyür; boyun da iki taraftan, orta noktasına doğru incelir. Olası bir başka örnek, bir manifoldda in­ce çubuk şeklinde çıkıntı olduğunda orta­ya çıkıyordu. Ricci akışı, bu durumda "puro tekilliği" adı verilen bir sorun oluş­turabilirdi. Manifold bu şekilde çimdik-lendiğinde ''tekil" niteliğini kazanır; artık gerçek bir üç boyutlu manifold değildir. Gerçek bir üç boyutlu manifoldda, her-

Geometrikleştirme

2-manifoldlar "tekbiçimleştirilerek" ya da "geometrikleştirilerek", yani onlara belirli bir geometri, ya da katı bir biçim tahsis ederek sınıflandırılabilirler. Her biri, eğriliği düzgün biçimde dağılmış bir şekle dö­nüşebilir. Küre (a) her noktada sabit pozitif eğriliği olan, yani her noktada bir tepenin üst bölümü gibi eğrilmiş yegane biçimdir. Tor (simit) (b) düz, yani her noktada eğriliği sıfır olan şekle getirilebilir. Bunu görmek İçin torun kesilip silindir

şeklinde uzatıldığını düşünün. Bu durumda da silindir, boylu boyunca kesilerek bir dikdörtgen düzlem parçasına dönüştürülebilir. Tür-2 ve daha yüksek türlere (c) sabit nega­tif eğrilik verilebilir; kulp sayısına bağlı olarak başka ayrıntılar da var­

dır. Burada sabit negatif eğrilik eyer şekliyle gösterilmiştir.

3-manifoldların sınıflandırılması da 2-manifoldlarınkine benzer; ama çok daha karmaşıktır. Bu sınıflan­dırma, Perelman'ın çalışmasıyla tamamlanmış bulunuyor. Genel olarak, bir 3-manifoldun parçalara ay­rılması, bu parçalardan her birine de, üç boyutlu sekiz doğal {"kanonik") geometriden birinin şeklinin verilebilmesi gerekir. Aşağıda verilen mavi renkli örnek (2-manifoldlar olarak art arda çizilmiş) beş ta­nesine denk olan geometrilerden oluşuyor: sabit pozitif (a), sıfır (b), negatif (c) eğrilikleri olan 3-geo-metriler, ayrıca 2-küre ile çember "çarpımı" (d) ve negatif eğriliği olan yüzeyle çember çarpımı (a).

3-manifold

3-manifoldlarm 2-manifoldlardan çok daha karışık olduğu anlaşılıyor. 3-mani-foldların çoğu tek bir geometriyle eşleş-mez; her birinin, farklı bir doğal ("kano-

lojik 3-manifoldu, eğriliğin manifold bo­yunca düzgün biçimde yayıldığı, tek bir geometriyle eşleştirmek mümkün mü­dür?

Aralık 2004 71 BİLİM ve TEKNİK

mektir ki, topolojik bakımdan bu mani­fold bir 3-küredir. Perelman'ın araştırması Poincare sa­vını İspatlamanın ötesinde, getirdiği yeni analiz teknikleri bakımından da önemli­dir. Matematikçiler onun çalışmasına da­yanan çalışmalar göndermeye, ya da onun tekniklerini başka problemlere uy­gulamaya başladılar bile. Ayrıca, bu ma­tematiğin fizikle de tuhaf bir bağlantısı var. Hamilton ve Perelman tarafından kullanılan Ricci akışı, renormalizasyon grubu denen ve etkileşimlerin gücünün çarpışma gücüne bağlı olarak nasıl değiş­tiğini belirleyen kavramla da bağlantılı. Örneğin, düşük enerjilerde elektroman­yetik etkileşim 0,0073 (yaklaşık 1 / 137) sayısıyla nitelenen bir güce sahiptir. An­cak, eğer ışık hızına yakın hızda iki elek­tron doğrudan çarpışırsa, güç 0,0078'e daha yakın olur. Çarpışma enerjisini artırmak, kuvveti daha kısa uzaklıklarda incelemek demek­tir. Bu nedenle, renormalizasyon grubu, bir süreci daha incelikli ya da kabaca iz­lemek için büyütmesi ayarlanabilen bir mikroskop gibidir. Benzer şekilde, Ricci akışı da, bir manifolda seçtiğiniz bir bü­yütme gücüyle bakmak gibidir. Bir bü­yütme ölçeğinde görülebilir olan girinti ve çıkıntılar bir başka ölçekte kaybolur. Fizikçiler, içinde yaşadığımız uzayın 10"35 metre, ya da Planck uzunluğu ölçeğinde çok farklı görünebileceğini düşünüyorlar ?bir sürü ilmeği, kulpu ve başka topolo­jik yapılan da olan bir "köpük". Fiziksel kuvvetlerin değişimiyle ilgili matematik, manifoldların geometrikleştirilmesiyle il­gili matematiğe çok benzer. Fizikle bir başka bağlantı da genel gö­relilik denklemleridir. Kütleçekim kuvve­tinin işleyişini ve evrenin büyük ölçekli yapısını açıklayan bu denklemler, Ricci akışı denklemiyle yakından ilişkilidir. Da­hası, Hamilton'un kullandığı temel akış denklemine Perelman'ın eklediği terim, kütleçekimin kuantum kuramı olan si­cim kuramında da ortaya çıkar. Perel­man'ın tekniklerinin genel görelilik ya da sicim kuramı hakkında ilginç, yeni bil­giler getirip getirmeyeceğini henüz bilmi­yoruz. Eğer bu gerçekleşirse, Perelman bize soyut 3-uzayların şekli konusunda bilgi vermiş olmanın yanısıra, içinde ya­şadığımız bu özel uzayın şekli konusun­da da bizi aydınlatmış olacak. Collins, G.P. "The Shapes of Space" Scientific American, Temmuz 2004 Çeviri: Nermin Arık

Tekilliklerle Başetmek

şılaşır. Bir örnek, haller şeklinde (bir tüple birleşen iki küre) şeklin­deki manifolddur (a). Tüp, bir noktada çimdiklendiğinde manifoldun özelliklerini bozar (b). Puro tekilliği denen bir başta tekilliğin de varolabileceği düşünülüyordu.

Perelman'ın çalışmalarından önce. Poincare savını ispatlamak ve 3-manifoldları geometrikleştirmek için Ricci akış denklemini kullanma çabaları, bir engele takılmıştı. Bir 3-manifoldun şeklini yavaş yavaş değiştiren Ricci akışı, arada "tekillikler" adı verilen sorunlarla kar-

Ricci akışı devam eder. Daha sonra başka bölgelerde de çimdik gö­rülürse bu sürecin birkaç kez tekrarlanması gerekebilir. Perelman, bu sürecin sonunda biteceğini kanıtladı. Aynı zamanda puro tekil­liklerinin de asla olmayacağını gösterdi.

"Ameliyat", Perelman'ın çalışmasında gösterildiği gibi. Ricci akışın­da ortaya çıkan tekillikler sorununu çözebilir. Manifoldun bir bölge­si çimdiklenmeye başladığında, bunun her iki tarafında küçük birer bölge kesilip çıkartılır |c); bu kesikler küçük kürelerle kapatılır ve

yımda Perelman, bağlı bulunduğu Stek-lov Enstitüsü dışında ABD'deki doktora sonrası pozisyonlarında biriktirdiği para­nın desteğini de dile getiriyordu. Perelman, makalesinde Ricci akışı denklemine bir terim eklemişti. Bu deği­şiklik, tekillik sorununu yok etmiyordu; ancak Perelman'ın 3-manifoldların anali­zini çok daha İleriye götürmesini sağlı-yor, halter türü tekilliklerde 'ameliyat' yapılabileceğini gösteriyordu. Ameliyat yöntemiyse halterdeki ince tüpü, çimdik-lenmenin başladığı noktanın iki yanın­dan kesip, her iki taraftaki açık tüpün ağ­zını küre biçiminde bir kapakla kapat­maktı. Bu durumda Ricci akışı, ameliyat­lı manifold İle, bir sonraki çimdiğe kadar devam eder; bu yeni çimdik için ameliyat tekrarlanır. Perelman bunun dışında, pu­ro tekilliklerinin oluşamayacağını da gös­terdi. Öyleyse, herhangi bir 3-manifold, her biri tekbiçim geometriye sahip parça­ların bir topluluğuna indirgenebilirdi. Ricci akışı ve ameliyat yöntemleri, ola­naklı bütün 3-manifoldlara uygulandığın­da, bir 3-küre kadar 'basit' (yani, 3-kürey-le aynı homotopiye sahip) herhangi bir manifold, mutlaka 3-küre gibi tekbiçim bir geometriye sahip olacaktır. Bu de-

hangi bir nokta çevresindeki küçük bir bölge, sıradan bir üç boyutlu uzayın kü­çük bir bölgesi gibi görünür; ancak çim-diklenmiş noktalarda bu özellik yoktur. İşte bu engeli ortadan kaldıracak yol, Pe-relman'ı beklemek zorundaydı. Perelman ABD'ye 1992 yılında dokto­ra sonrası öğrencisi olarak geldi. New York Üniversitesi ve Stony Brook'da bir­kaç yan-yıl kaldıktan sonra Berkeley'de-ki California Üniversitesi'nde iki yıl geçir­di. Kısa sürede, geometrinin belirli bir dalında önemli sonuçlar ispatlayarak, parlak bir genç yıldız olarak ünlendi. Av­rupa Matematik Derneği'nin ona verdiği ödülü reddetse de, Uluslararası Matema­tikçiler Kongresi'ne bir konferans verme­si için kendisine yapılan oldukça prestijli teklifi kabul etti. 1995 baharında, Önde gelen matematik bölümlerinin kendisine yaptığı kadro tekliflerini de geri çeviren Perelman, ülkesine, St. Petersburg'a ge­ri döndü. Amerikalı meslektaşlarından biri onun İçin "Kültür bakımından tam bir Rus. Materyalizmden çok uzak" de­mişti. Petersburg'a döndükten sonra Perel­man, matematikçilerin radar ekranların­da pek görünmez olmuştu. Yıllar sonra, eski meslektaşlarına ender olarak elek­tronik posta mesajları göndererek, söz­gelimi İnternet'te yayımlanmış makalele-rindeki hatalara dikkat çekmek dışında sesi pek çıkmadı. Kendisinin neler yaptı­ğını soran mesajlarsa yanıtsız kalıyordu. Nihayet 2002 sonlarında birkaç kişi ondan e-posta alabildi. Ortak matematik sunucusuna gönderdiği çalışmayı haber veriyor ve kendine özgü üslubuyla, kısa­ca, makaleye ilgi duyabileceklerini söylü­yordu. Bu mesaj, onun Poincare savıyla uğraştığının İlk habercisiydi. Bu ön ya-

BİLİM veTEKNİK 72 Aralık 2004