MATEMATİK

MÜZİK

ANALIZ

(x+3).5=x-4 İşte çevirme işi tamamlandı. Bundan sonrası yani denklem çözümü matemati­ğin işi. Sonuca ulaşınca onu da Türkçe-ye çeviririz. Galileo "Doğanın muazzam kitabının dili matematiktir'' derken matematiğin başlı başına bir dil olduğunu açıkça ifade etmiştir. Matematiğin de bir dil olduğu üzerine bu kadar yazdıktan sonra bu di­li öğretmeye çalışacağımı sanıyorsanız, üzgünüm ki sizi hayal kırıklığına uğrata­cağım. Çünkü bu, matematikçilerin işi. Ben daha çok hangi dillerin matematiğe çevrileceği konusu üzerinde durmak isti­yorum. Tabii ki Türkçe çevrilebiliyorsa bütün konuşma dilleri de çevrilebilir, ya başka?!!...

ğini inceleyeceğiz.(Sabır istiyorum çün­kü yaptıklarımız size önce alakasız gibi görünebilir) Biraz Fizik Önce sesin ne olduğuna dair bilgileri­mizi tazeleyelim sonra da müzik ile gü­rültü arasındaki ayırımı yapabiliriz. Duy­duğumuz ses, titreşen nesnelerin yarattı­ğı ses dalgalarının hava aracılığı ile kula­ğımıza ulaşmasıdır dersem sesi çok da­raltarak açıklamış olurum ama şimdilik bu kadarlık bilgi yeterli olur. (örneğin aracı olarak sadece hava demek eksik olur. Katı, sıvı ve gazlar aracı olabilirler). Öyleyse ses dalgalar halinde yayılır. Me­sela bir gitarı çaldığımızda titreşen teller, hava moleküllerinin aynı şekilde titreşe-

Matematiğin derin felsefesini arılama­ya çalıştığım öğrencilik günlerimden ak­lımda belki de hayat boyu silinmeyecek bazı anılar kaldı. Bunlardan biri de za­manımın ve paramın çoğunu harcadığım kırtasiye dükkanında geçiyor. Kitabımın eksik basılmış sayfalarını çektirmek üze­re her zaman gittiğim kırtasiyede fotoko­pilerimin çekilmesini bekliyordum. Bu arada da gözümü etrafta gezdirip alış ve­riş açlığımı nasıl doyurabilirim acaba di­ye raflara bakmaktan da geri kalmıyor­dum. Tam bu sırada içeriye mahallenin delikanlısı tavırlarında tipik bir genç gir­di. Kendine has bir selamı İşini yapmak­ta olan arkadaşına verdikten sonra foto­kopisini çektiği kitaba biraz daha yakın­dan bakmak İçin eğildi."Demek Arapça kitapların da fotokopisini çekiyorsun"

rek birbirine çarpmasını sağlar. Yani teller enerjisini o molekül­lere aktarır. Her molekül bir di­ğerini titreştirerek bu dalgaların kulak kepçemize kadar ulaşma­sını sağlar.

dedi bilgiç bir tavırla. Gözle­rim fal taşı gibi açılmış          onları izlerken arkada­şının karizmasını dağıt-                  z \oof\ F mak istemeyen dükkan i z<Oj sahibi eliyle ağzını kapa­tarak "Yok oğlum, bu mate- Zo>hPk matik kitabı"dedi...Üniversi- A'* r&>, teye ilk adım attığım hafta­larda bana da garip gel­mişti karşıma çıkan mate­matik kitapları. İçlerinde bir sürü garip sembol ve tanınmadık harfler, (a ve |3 yetmemiş bütün Yunan al­

Biraz da Biyoloji Sesler yani dalgalar yeterin­ce güçlü ise kulak kepçesinde toplanır ve dış kulak yoluna iletilir. Bu kanalın sonunda yer alan kulak zarına ulaşan titreşirn-ler ortakulaktaki çekiç-örs-özengi

fabesinin harflerini kullanmışlar­dı) Üstelik bazılarında sayfa numara­

adlı kemikleri (aynı şekilde) titreş­tirdikten sonra oval pencere adlı zara ge­tirilir, buradan da iç kulağa aktarılır. Tit­reşimler, iç kulak kanallarındaki sıvılar­da dalgalar halinde ilerleyerek Corti or­ganını uyarır. Uyarılar sinirlerle beyne taşınarak gitar tellerinden çıkan melodi­nin İşitilmesi sağlanır. Anlatması uzun sürdü ama bu, saliseler içinde gerçekle­şen bir olay.

sından başka sayı da yok diye söylenir­dim kendi kendime. Ama yine de Arap Alfabesini aldırdığını hiç düşünmemiş­tim doğrusu... Aslında durum oldukça açıktı. Bilme­diğin, tanımadığın bir dili ne yazabilir­sin, ne konuşabilirsin, ne de okuyabilir­sin, emek verip öğrenmek gerektirir. Ak­si halde bir tercümana ihtiyaç duyarsın. Matematiğin de kendine has bir dili var. Nasıl Türkçeyi İngilizceye çeviriyorsak, Türkçeyi ya da başka herhangi bir dili (bir karşılığı varsa eğer) matematiğe çe­virebiliriz. Nasıl mı? Basit! Aslında bu işi 6.sınıftan beri problemler adı altında öğ­reniyoruz; Bir sayının 3 fazlasının 5 katı, kendi­sinin 4 eksiğine eşittir. Bu sayı kaçtır? Şeklinde bir soruyu hatırlayın. Bir sayı emektar 'x' idi.

Biraz Müzik Hep düşünmüşümdür matematik ve müzik arasındaki İlişkiyi. Çünkü çok ala­kalı olduğu söylenir ama müzik öğret­menlerimden aldığım cevaplar bana hiç de öyle alakalı olduklarını düşündürtme-miştir. Sol anahtarının yanına yazılan birkaç rakamdan ya da notaların, susla-rın adına verilen oranlardan ve sayılar­dan ibaret ise bence üzerine bu kadar konuşmaya değmezdi. O zaman kendi başımın çaresine bakıp konuyu daha te­melden İncelemeye başlamak durumun­daydım. Çünkü müzik dilinin kurallarını bilmeden onun matematik diline nasıl çevrildiğini anlayamazdım. Galiba sonun­da ağzımdaki baklayı çıkardım. Biraz­dan, sabırla birkaç bilgiyi öğrendikten sonra, müziğin matematiğe nasıl çevrildi-

Artık Biraz da Matematik Gitar telleri titreşedursun, biz biraz da matematik yapmaya koyulalım. İşe pe­riyodik fonksiyonun tanımıyla başlayabi­liriz. Bir f fonksiyonu alalım öyle olsun ki f:A->B,VxeA için f{x)=f{x+T)

BİLİM ve TEKNİK 74 Kasım 2004

Eşitliğini sağlayan sabit bir T sayısı bulunsun. F fonksiyonuna periyodik fonksiyon, T'ye de f fonksiyonunun peri­yodu denir. Yani periyot kelimesinin sez­dirdiği üzere fonksiyon kendini T kadar­da bir tekrarlıyor. Bizim işimize lazım olan, kendisini T zamanda bir tekrarla-yan fonksiyonlardır. Hazır yeri gelmiş­ken şunu da söylemeden geçemeyece­ğim; İki periyodik fonksiyonun toplamı da periyodik bir fonksiyon verir( bu yeni fonksiyonun periyodu ayrı ayrı periyotla­rın toplamına eşit değildir, O.K.E.K.leri-ne eşittir). 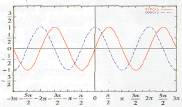Yine fizik derslerinden hatırlarsanız frekans da periyodun çarpmaya göre ter­si İdi: F=l/T Matematikte en sık karşılaşılan periyo­dik fonksiyonlar periyodu 2pi (haliyle fre­kansı da l/2pi) olan sinüs ve kosinüs fonk­siyonlarıdır. Belki emektar matematik öğ­retmenlerimizin dalgalanan grafikler diye aklımıza sokmaya çalıştıkları bu grafikle­rin görüntülerini hatırlayanınız vardır.

dilin birbirine nasıl çevrildiğini anlayabi­liriz Joseph Fourier'in 19. Yüzyılda söyle­diği şuydu: Neredeyse her periyodik fonksiyon sinüs ve kosinüs fonksiyonları cinsinden sonsuz serilerle açılabilir. Da­ha somut olarak; müzik aleti ve İnsan­dan çıkan bütün müzikal sesler (periyo­dik oldukları için) matematiksel ifadelere dönüşebilir ki bunlar da sinüs ve kosi­nüs fonksiyonlarıdır. Öyleyse çıkaracağınız bir do sesinin aşağıdaki türden bir ifadeye denk olması mümkün: y(t) = l/2a0 + (a1 cos t + b1 sin t) + (a2 cos 2t + b2 sin t) + ... + (an cos nt + bn sin nt), ya da =Tan cos nt +bn sin nt

Do,Re,...,La,Si

Hazır bu kadar bilgiyi edinmişken sı­cağı sıcağına notalardan bahsetmeden bu konuyu kapatmak olmaz. Çünkü mü­zik ile her hangi bir sesin nasıl ayırt edil­diğini anlamamız için nota bilgisine de ihtiyacımız var. Kulaklarımız bu ikisini kolayca ayırt ediyor olabilir, peki ya ma­tematiksel ifadelerle karşı karşıya isek işin içinden nasıl çıkarız? Notalar fre­kansları birbirlerine oranlanınca rasyo­nel sayı veren ses dalgalarından oluşur. Bugün kullandığımız 7 notalı sisteme ba­karsak do sesini veren frekansın 9/8'i reyi ya da 3/2 sol sesini vermektedir. Do sesinin frekansı 264Hz olarak ölçüldü­ğüne göre RE 297 sol de 396Hz olarak basitçe hesaplanabilir. Hangi do? Bir piyano klavyesine baktığımızda bir sürü do görebiliriz hepsinin sesi de farklı ama aynı. Bu ne demek açıklaya-mam ama birisinin ince diğerinin kalın do olduğunu kulaklarımız zaten anlıyor. Biz aralarındaki matematiksel ilişkiyi in­celiyoruz. Kalın do 264Hz iken ince do 528 Hz olarak ölçütür. Yani 528:264=2. İşte iki sesin frekans oranı tam sayı İse biri diğerinden oktav farkı ile kalın olu-yor. Bu Örnekte aralarında 1 oktav var, Oran 3 olsaydı aralarında 2 oktav var di­yecektik.

İşte her hangi bir periyodik fonksiyo­na uyarlamak için bu denklemlerde veri­len ve Fourier katsayıları olarak bilinen an ve bn değerlerini bulmaya Fourier Analiz diyoruz. Fourier Analiz müzikte bir sesin temel bileşeniyle harmonikleri-ne ayrılmasında kullanıldığı için Harmo-nik Analiz olarak da anılır. Yukarıdaki sonsuz seriye de Fourier Serisi deniyor. Artık her müziğin matematiğe dönüştü­rülebileceğini biliyoruz. Peki ya geri dö­nüş? Geri Dönüşüm Şimdiye kadar hep müziğin matemati­ğe dönüşümünden bahsettik. Peki geri dönüşüm nasıl olacak. Aslında bu işi ya­pan aletlerden bahsedersek durumu ol­dukça somutlaştırmış oluruz. Doktorun hastasına, onun kalp atışlarını izlemek için taktığı EKG cihazının monitöre yan­sıyan görüntüsü en azından filmlerden izleyeniniz varsa bilir. Hani hastayı kay­bedince kalp durduğu ve hiç ses gelme­diği İçin ekranda düz bir çizgi geçer. İş­te o zaman yukarıdaki tüm Fourier kat­sayıları sıfır olur. Örneğin sin(x) grafiğini çalma şansı­mız olsa onun frekansında ve dalga bo­yundaki bir ses dalgası nasıl bir ses çıka­rır. Gitarın saniyedeki titreşim sayısını ayarlayacak şekilde dokunabilseydik bu­nu yapabilirdik. Ama 1 saniyede ne ka­dar titreştiğini bile sayamayan beyinleri­miz bunu da başaramaz. Ama başaran aletleri yani bilgisayarları üretmekten de geri kalmazlar! Size bu konuda yardımcı olması için ancak internet adresi verebi­lirim. Böylece sin(x) ya da 4sin2(x) grafi­ğinin sesini (program indirmeden) dinle­yebilirsiniz: http://librat7.thinkquest.org/ 19537/java/Wave. html

Ses Dalgası ve Dalgalanan grafikler Sanırım yavaş yavaş sadede geliyo­rum. Şimdi gitar teline geri dönelim ve artık öğrendiklerimizi hayata geçirelim. Telin 1 saniyedeki titreşim sayısı bize duyduğumuz sesin (ya da kulak kepçe­mize yaklaşmakta olan dalganın) frekan­sını verecektir. Frekansı 19. 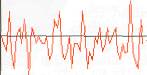Yüzyılda radyo dalgalarının nasıl oluştuğunu keş­feden bilim adamına ithafen Hertz ile öl­çüyoruz 1 Hertz=l titreşim/saniye Telin saniyede 300Hz ile titreşmeye başladığını farz edelim. O sırada yanı ba­şında bulunan hava molekülü de 300Hz ile titreşir ve o da yanındakini 300Hz ile titreştirir derken biraz önce anlattığımız olaylar gerçekleşir. Peki bir şansımız ol­sa da çıkan bu ses dalgasının fotoğrafını çeksek, nasıl bir görüntüyle karşılaşırız? Aşağıda bir trompetten çıkan bir notanın ya da ses dalgasının resmi var! Dalgala­

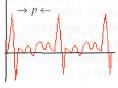
gürültünün resmi Sonuç olarak müzik, frekans oranları rasyonel olan notaların bir karışımıdır. Gürültü de çıkan sesler de ise frekans oranlarında pek bir matematiksel düzen bulmak mümkün değildir. Kiminin bayı­larak dinlediği müzik kimine gürültü olarak gelebilir. Evdekiler ben müzik dinlerken " şu gürültüyü kapat da kafa­mız rahat etsin" dediklerinde onlara ma­tematiksel oranlardan bahsetmeye başlı­yorum. İşte o zaman müziğimi dinlemeyi tercih ediyorlar. Hayır oranları sevimli bulduklarından değil, aksine matematik dinlemektense gürültüyü dinlemeyi ter­cih ettiklerinden. İşte böyle zamanlarda matematiğin ürkütücü(!) görünmesinden hoşlanıyorum. Tavsiye ederim! Nilüfer Karadağ karadagnilufer@yahoo.com

nan grafikleri andırmıyor mu? Öyleyse son bir teorem yaz­dıktan sonra iki

Kasım 2004 75 BİLİM ve TEKNİK